Part 1: Lagrange Duality¶
In this lecture, we continue looking at Support Vector Machines (SVMs), and define a new formulation of the max-margin problem.
Before we do that, we start with a general concept -- Lagrange duality.
Review: Maximizing the Margin¶
We saw that maximizing the margin of a linear model amounts to solving the following optimization problem. \begin{align*} \min_{\theta,\theta_0} \frac{1}{2}||\theta||^2 \; & \\ \text{subject to } \; & y^{(i)}((x^{(i)})^\top\theta+\theta_0)\geq 1 \; \text{for all $i$} \end{align*}
We are going to look at a different way of optimizing this objective. But first, we start by defining Lagrange duality.
Constrained Optimization Problems¶
We will look at constrained optimization problems of the form \begin{align*} \min_{\theta \in \mathbb{R}^d} \; & J(\theta) \\ \text{such that } \; & c_k(\theta) \leq 0 \text{ for $k =1,2,\ldots,K$} \end{align*} where $J(\theta)$ is the optimization objective and each $c_k(\theta) : \mathbb{R}^d \to \mathbb{R}$ is a constraint.
Our goal is to find a small value of $J(\theta)$ such that the $c_k(\theta)$ are negative.
Optimization with Penalties¶
Another way of approaching the above goal is via: $$\min_\theta \mathcal{L}(\theta, \lambda) = J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta)$$ for some positive vector of Lagrange multipliers $\lambda \in [0, \infty)^K$. We call $\mathcal{L}(\theta, \lambda)$ the Lagrangian.
- If $\lambda_k \geq 0$, then we penalize large values of $c_k$
- For large enough $\lambda_k$, no $c_k$ will be positive --- a valid solution.
Penalties are another way of enforcing constraints.
Penalties vs. Constraints¶
Penalites and constraints are closely related. Consider our constrained optimization problem: \begin{align*} \min_{\theta \in \mathbb{R}^d} \; & J(\theta) \\ \text{such that } \; & c_k(\theta) \leq 0 \text{ for $k =1,2,\ldots,K$} \end{align*}
We define its primal Lagrange form to be $$\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \left(J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta) \right)$$
These two forms have the same optimum $\theta^*$!
Why is this true? Consider again $$\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \left(J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta) \right)$$
- If a $c_k$ is violated ($c_k > 0$) then $\max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda)$ is $\infty$ as $\lambda_k \to \infty$.
- If no $c_k$ is violated and $c_k < 0$ then the optimal $\lambda_k = 0$ (any other value makes the objective smaller).
- If $c_k < 0$ for all $k$ then $\lambda_k=0$ for all $k$ and $$\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} J(\theta)$$
Thus, $\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta)$ is the solution to our initial optimization problem.
Langrange Dual¶
Now consider the following problem over $\lambda\geq 0$: $$\max_{\lambda \geq 0}\mathcal{D}(\lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta, \lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \left(J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta) \right).$$
We call this the Lagrange dual of the primal optimization problem $\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta)$. We can always construct a dual for the primal.
Lagrange Duality¶
The dual interesting because we always have: $$ \max_{\lambda \geq 0}\mathcal{D}(\lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \leq \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta)$$
Moreover, in many interesting cases, we have $$ \max_{\lambda \geq 0}\mathcal{D}(\lambda) = \min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta).$$ Thus, the primal and the dual are equivalent!
Example: Regularization¶
Consider regularized supervised laerning problem with a penalty term: $$ \min_{\theta \in \Theta} L(\theta) + \lambda \cdot R(\theta). $$
We may also enforce an explicit constraint on the complexity of the model: \begin{align*} \min_{\theta \in \Theta} \; & L(\theta) \\ \text{such that } \; & R(\theta) \leq \lambda' \end{align*} We will not prove this, but solving this problem is equivalent so solving the penalized problem for some $\lambda > 0$ that's different from $\lambda'$.
In other words, we can regularize by explicitly enforcing $R(\theta)$ to be less than a value or we can penalize $R(\theta)$.
We are now going to see another application of Lagrangians in the context of SVMs.
Review: Binary Classification¶
Consider a training dataset $\mathcal{D} = \{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(n)}, y^{(n)})\}$.
We distinguish between two types of supervised learning problems depnding on the targets $y^{(i)}$.
- Regression: The target variable $y \in \mathcal{Y}$ is continuous: $\mathcal{Y} \subseteq \mathbb{R}$.
- Binary Classification: The target variable $y$ is discrete and takes on one of $K=2$ possible values.
In this lecture, we assume $\mathcal{Y} = \{-1, +1\}$.
Review: Linear Model Family¶
In this lecture, we will work with linear models of the form: \begin{align*} f_\theta(x) & = \theta_0 + \theta_1 \cdot x_1 + \theta_2 \cdot x_2 + ... + \theta_d \cdot x_d \end{align*} where $x \in \mathbb{R}^d$ is a vector of features and $y \in \{-1, 1\}$ is the target. The $\theta_j$ are the parameters of the model.
We can represent the model in a vectorized form \begin{align*} f_\theta(x) = \theta^\top x + \theta_0. \end{align*}
Review: Geometric Margin¶
We define the geometric margin $\gamma^{(i)}$ with respect to a training example $(x^{(i)}, y^{(i)})$ as $$ \gamma^{(i)} = y^{(i)}\left( \frac{\theta^\top x^{(i)} + \theta_0}{||\theta||} \right). $$ This also corresponds to the distance from $x^{(i)}$ to the hyperplane.
Review: Maximizing the Margin¶
We saw that maximizing the margin of a linear model amounts to solving the following optimization problem. \begin{align*} \min_{\theta,\theta_0} \frac{1}{2}||\theta||^2 \; & \\ \text{subject to } \; & y^{(i)}((x^{(i)})^\top\theta+\theta_0)\geq 1 \; \text{for all $i$} \end{align*}
We are going to look at a different way of optimizing this objective. But first, we start by defining Lagrange duality.
Review: Penalties vs. Constraints¶
Penalites and constraints are closely related. Consider our constrained optimization problem: \begin{align*} \min_{\theta \in \mathbb{R}^d} \; & J(\theta) \\ \text{such that } \; & c_k(\theta) \leq 0 \text{ for $k =1,2,\ldots,K$} \end{align*}
We define its primal Lagrange form to be $$\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \left(J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta) \right)$$
These two forms have the same optimum $\theta^*$!
The Lagrangian of the SVM Problem¶
Consider the following objective, the Langrangian of the max-margin optimization problem.
\begin{align*} L(\theta, \theta_0, \lambda) = \frac{1}{2}||\theta||^2 + \sum_{i=1}^n \lambda_i \left(1-y^{(i)}((x^{(i)})^\top\theta+\theta_0)\right) \end{align*}Intuitively, we have put each constraint inside the objective function and added a penalty $\lambda_i$ to it.
Review: Langrange Dual¶
Consider the following problem over $\lambda\geq 0$: $$\max_{\lambda \geq 0}\mathcal{D}(\lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \mathcal{L}(\theta, \lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \left(J(\theta) + \sum_{k=1}^K \lambda_k c_k(\theta) \right).$$
We call this the Lagrange dual of the primal optimization problem $\min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta)$. We can always construct a dual for the primal.
The Dual of the SVM Problem¶
Consider optimizing the above Lagrangian over $\theta, \theta_0$ for any value of $\lambda$. $$\min_{\theta, \theta_0} L(\theta, \theta_0, \lambda) = \min_{\theta, \theta_0} \left( \frac{1}{2}||\theta||^2 + \sum_{i=1}^n \lambda_i \left(1-y^{(i)}((x^{(i)})^\top\theta+\theta_0)\right)\right)$$ This objective is quadratic in $\theta$; hence it has a single minimum in $\theta$.
We can find it by setting the derivative to zero and solving for $\theta, \theta_0$. This yields: \begin{align*} \theta & = \sum_{i=1}^n \lambda_i y^{(i)} x^{(i)} \\ 0 & = \sum_{i=1}^n \lambda_i y^{(i)} \end{align*}
Substituting this into the Langrangian we obtain the following expression for the dual $\max_{\lambda\geq 0} \mathcal{D}(\lambda) = \max_{\lambda\geq 0} \min_{\theta, \theta_0} L(\theta, \theta_0, \lambda)$: \begin{align*} \max_{\lambda} & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{k=1}^n \lambda_i \lambda_k y^{(i)} y^{(k)} (x^{(i)})^\top x^{(k)} \\ \text{subject to } \; & \sum_{i=1}^n \lambda_i y^{(i)} = 0 \\ & \lambda_i \geq 0 \; \text{for all $i$} \end{align*}
Lagrange Duality in SVMs¶
Recall that in general, we have: $$ \max_{\lambda \geq 0}\mathcal{D}(\lambda) = \max_{\lambda \geq 0} \min_{\theta \in \mathbb{R}^d} \leq \min_{\theta \in \mathbb{R}^d} \max_{\lambda \geq 0} \mathcal{L}(\theta, \lambda) = \min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta)$$
In the case of the SVM problem, one can show that $$ \max_{\lambda \geq 0}\mathcal{D}(\lambda) = \min_{\theta \in \mathbb{R}^d} \mathcal{P}(\theta).$$ Thus, the primal and the dual are equivalent!
Properties of the Dual¶
We can make several observations about the dual \begin{align*} \max_{\lambda} & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{k=1}^n \lambda_i \lambda_k y^{(i)} y^{(k)} (x^{(i)})^\top x^{(k)} \\ \text{subject to } \; & \sum_{i=1}^n \lambda_i y^{(i)} = 0 \;\text{and}\; \lambda_i \geq 0 \; \text{for all $i$} \end{align*}
- This is a constrainted quadratic optimization problem.
- The number of variables $\lambda_i$ equals $n$, the number of data points.
- Objective only depends on products $(x^{(i)})^\top x^{(j)}$ (more on this soon!)
When to Solve the Dual¶
When should we be solving the dual or the primal?
- The dimensionality of the primal depends on the number of features. If we have a few features and many datapoints, we should use the primal.
- Conversely, if we have a lot of features, but less datapoints, we want to use the dual.
In the next lecture, we will see how we can use this property to solve machine learning problems with a very large number of features (even possibly infinite!).
Part 3: Practical Considerations for SVM Duals¶
We continue our discussion of the dual formulation of the SVM with additional practical details about the dual formulation is defined an used.
Review: Binary Classification¶
Consider a training dataset $\mathcal{D} = \{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \ldots, (x^{(n)}, y^{(n)})\}$.
We distinguish between two types of supervised learning problems depnding on the targets $y^{(i)}$.
- Regression: The target variable $y \in \mathcal{Y}$ is continuous: $\mathcal{Y} \subseteq \mathbb{R}$.
- Binary Classification: The target variable $y$ is discrete and takes on one of $K=2$ possible values.
In this lecture, we assume $\mathcal{Y} = \{-1, +1\}$.
Review: Primal and Dual Formulations¶
Recall that the the max-margin hyperplane can be formualted as the solution to the following primal optimization problem. \begin{align*} \min_{\theta,\theta_0} \frac{1}{2}||\theta||^2 \; & \\ \text{subject to } \; & y^{(i)}((x^{(i)})^\top\theta+\theta_0)\geq 1 \; \text{for all $i$} \end{align*}
The solution to this problem also happens to be given by the following dual problem: \begin{align*} \max_{\lambda} & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{k=1}^n \lambda_i \lambda_k y^{(i)} y^{(k)} (x^{(i)})^\top x^{(k)} \\ \text{subject to } \; & \sum_{i=1}^n \lambda_i y^{(i)} = 0 \\ & \lambda_i \geq 0 \; \text{for all $i$} \end{align*}
Review: Non-Separable Problems¶
Our dual problem assumes that a linear hyperplane exists. However, what if the classes are non-separable? Then our optimization problem does not have a solution and we need to modify it.
Our solution is going to be to make each constraint "soft", by introducing "slack" variables, which allow the constraint to be violated. $$ y^{(i)}((x^{(i)})^\top\theta+\theta_0)\geq 1 - \xi_i. $$
In the optimization problem, we assign a penalty $C$ to these slack variables to obtain: \begin{align*} \min_{\theta,\theta_0, \xi}\; & \frac{1}{2}||\theta||^2 + C \sum_{i=1}^n \xi_i \; \\ \text{subject to } \; & y^{(i)}((x^{(i)})^\top\theta+\theta_0)\geq 1 - \xi_i \; \text{for all $i$} \\ & \xi_i \geq 0 \end{align*}
This is the primal problem. Let's now form its dual.
Non-Separable Dual¶
We can also formulate the dual to this problem. First, the Lagrangian $L(\lambda, \mu,\theta,\theta_0)$ equals \begin{align*} \frac{1}{2}||\theta||^2 + C \sum_{i=1}^n \xi_i - \sum_{i=1}^n \lambda_i \left(y^{(i)}((x^{(i)})^\top\theta+\theta_0)- 1\right) - \sum_{i=1}^n \mu_i\xi_i. \end{align*}
The dual objective of this problem will equal $$\mathcal{D}(\lambda, \mu) = \min_{\theta,\theta_0} L(\lambda, \mu,\theta,\theta_0).$$
As earlier, we can solve for the optimal $\theta, \theta_0$ in closed form and plug back the resulting values into the objective.
We can then show that the dual takes the following form: \begin{align*} \max_{\lambda} & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{k=1}^n \lambda_i \lambda_k y^{(i)} y^{(k)} (x^{(i)})^\top x^{(k)} \\ \text{subject to } \; & \sum_{i=1}^n \lambda_i y^{(i)} = 0 \\ & C \geq \lambda_i \geq 0 \; \text{for all $i$} \end{align*}
Coordinate Descent¶
Coordinate descent is a general way to optimize functions $f(x)$ of multiple variables $x \in \mathbb{R}^d$:
- Choose a dimension $j \in \{1,2,\ldots,d\}$.
- Optimize $f(x_1, x_2, \ldots, x_j, \ldots, x_d)$ over $x_j$ while keeping the other variables fixed.
Here, we visualize coordinate descent applied to a 2D quadratic function.
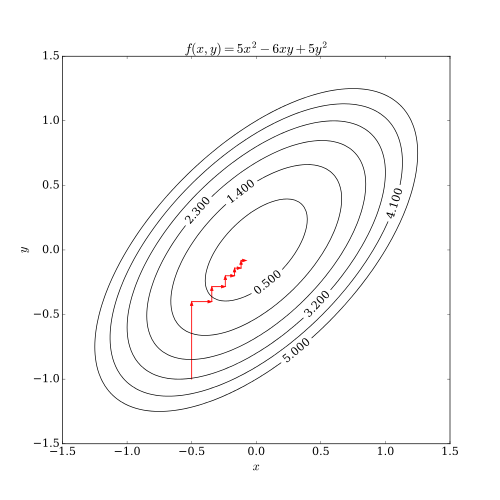
Sequential Minimal Optimization¶
We can apply a form of coordinate descent to solve the dual: \begin{align*} \max_{\lambda} & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{k=1}^n \lambda_i \lambda_k y^{(i)} y^{(k)} (x^{(i)})^\top x^{(k)} \\ \text{subject to } \; & \sum_{i=1}^n \lambda_i y^{(i)} = 0 \;\text{and}\; C \geq \lambda_i \geq 0 \; \text{for all $i$} \end{align*}
A popular, efficient algorithm is Sequential Minimal Optimization (SMO):
- Take a pair $\lambda_i, \lambda_j$, possibly using heuristics to guide choice of $i,j$.
- Reoptimize over $\lambda_i, \lambda_j$ while keeping the other variables fixed.
- Repeat the above until convergence.
Obtaining a Primal Solution from the Dual¶
Next, assuming we can solve the dual, how do we find a separating hyperplane $\theta, \theta_0$?
Recall that we already found an expression for the optimal $\theta^*$ (in the separable case) as a function of $\lambda$: $$ \theta^* = \sum_{i=1}^n \lambda_i y^{(i)} x^{(i)}. $$
Once we know $\theta^*$ it easy to check that the solution to $\theta_0$ is given by $$ \theta_0^* = -\frac{\max_{i:y^{(i)}=-1} (\theta^*)^\top x^{(i)} + \min_{i:y^{(i)}=-1} (\theta^*)^\top x^{(i)}}{2}. $$
Support Vectors¶
A powerful property of the SVM dual is that at the optimum, most variables $\lambda_i$ are zero! Thus, $\theta$ is a sum of a small number of points: $$ \theta^* = \sum_{i=1}^n \lambda_i y^{(i)} x^{(i)}. $$
The points for which $\lambda_i > 0$ are precisely the points that lie on the margin (are closest to the hyperplane).
These are called support vectors.
Notation and The Iris Dataset¶
To demonstrate how to use the dual version of the SVM, we are going to again use the Iris flower dataset.
We will look at the binary classificaiton version of this dataset.
import numpy as np
import pandas as pd
from sklearn import datasets
# Load the Iris dataset
iris = datasets.load_iris(as_frame=True)
iris_X, iris_y = iris.data, iris.target
# subsample to a third of the data points
iris_X = iris_X.loc[::4]
iris_y = iris_y.loc[::4]
# create a binary classification dataset with labels +/- 1
iris_y2 = iris_y.copy()
iris_y2[iris_y2==2] = 1
iris_y2[iris_y2==0] = -1
# print part of the dataset
pd.concat([iris_X, iris_y2], axis=1).head()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | -1 |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | -1 |
| 8 | 4.4 | 2.9 | 1.4 | 0.2 | -1 |
| 12 | 4.8 | 3.0 | 1.4 | 0.1 | -1 |
| 16 | 5.4 | 3.9 | 1.3 | 0.4 | -1 |
Let's visualize this dataset.
# https://scikit-learn.org/stable/auto_examples/neighbors/plot_classification.html
%matplotlib inline
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [12, 4]
import warnings
warnings.filterwarnings("ignore")
# create 2d version of dataset and subsample it
X = iris_X.to_numpy()[:,:2]
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, .02), np.arange(y_min, y_max, .02))
# Plot also the training points
p1 = plt.scatter(X[:, 0], X[:, 1], c=iris_y2, s=60, cmap=plt.cm.Paired)
plt.xlabel('Petal Length')
plt.ylabel('Petal Width')
plt.legend(handles=p1.legend_elements()[0], labels=['Setosa', 'Not Setosa'], loc='lower right')
<matplotlib.legend.Legend at 0x120be94e0>
We can run the dual version of the SVM by importing an implementation from sklearn:
#https://scikit-learn.org/stable/auto_examples/svm/plot_separating_hyperplane.html
from sklearn import svm
# fit the model, don't regularize for illustration purposes
clf = svm.SVC(kernel='linear', C=1000) # this optimizes the dual
# clf = svm.LinearSVC() # this optimizes for the primal
clf.fit(X, iris_y2)
plt.scatter(X[:, 0], X[:, 1], c=iris_y2, s=30, cmap=plt.cm.Paired)
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
# plot decision boundary and margins
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=100,
linewidth=1, facecolors='none', edgecolors='k')
plt.xlim([4.6, 6])
plt.ylim([2.25, 4])
plt.show()
Algorithm: Support Vector Machine Classification (Dual Form)¶
- Type: Supervised learning (binary classification)
- Model family: Linear decision boundaries.
- Objective function: Dual of SVM optimization problem.
- Optimizer: Sequential minimial optimization.
- Probabilistic interpretation: No simple interpretation!
